이진탐색 Binary Search : 정렬된 배열에서 탐색 범위를 절반씩 좁혀가며 데이터를 찾는 것
시간복잡도 : O(log N)

중복에 대해 고려하지 않은 경우
- 찾고자하는 key가 존재하는지만 알아내면 됨
- 메커니즘
1. 탐색 범위 내의 배열의 중간 인덱스를 구한다.
2. 중간 인덱스의 값과 key의 값을 비교한다.
3. 값이 중간 값보다 작다면 왼쪽 부분을, 크다면 오른쪽 부분을 탐색하고, 같다면 해당 인덱스를 반환하고 종료한다.
- 주의! 자료형의 최댓값 넘지 말기
보통 mid = (start + end) / 2 라고 표현하지만, 만약에 start + end 가 자료형의 최댓값을 넘어선다면 자바에서는 Overflow 오류가 발생
-> mid = start + (end - start) / 2 로 표현하면 오버플로를 피하면서 정확한 mid 값을 구할 수 있음
- 아래 코드에서는 while문 조건에 따라 각각 코드를 정리하였다.
- 또한, 값이 없는 경우 -1을 반환하거나 key보다 큰 값 혹은 작은 값을 반환하는 경우도 정리하였다.
static int binarySearch1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid;
else if(key == arr[mid]) return mid; //값 인덱스 반환
else start = mid + 1;
}
return -1; //존재하지 않는 경우 -1 반환
}
static int binarySearch2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return -1;
}// 중복이 없을 경우 key 보다 크거나 같은 위치
static int greaterThanOrEqualTo(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return start;
}
// 중복이 없을 경우 key 보다 작거나 같은 위치
static int smallerThanOrEqualTo(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return end;
}
Arrays.binarySearch() 메소드
Arrays.binarySearch(int[] a, int key); // a는 배열, key는 찾고자 하는 값
- 아주 조금 빠르지만 왠만하면 직접 구현하는 편이 나음
- 해당 key를 찾으면 위치 반환(값이 여러개라면 무작위)
- 값이 없으면 -(InsertionPoint + 1) 반환
- InsertionPoint = key 보다 큰 최초의 위치
- 아래는 arr={1,2,2,4,4,4,6,7,7,9}; key=3일 경우의 예시 Arrays.binarySearch(arr,3) = -4

중복에 대해 고려한 경우
lower bound 하한 : 찾고자 하는 값 이상의 값이 처음으로 나타나는 위치
upper bound 상한 : 찾고자 하는 값 초과한 값이 처음으로 나타나는 위치
- 값이 없어도 그것보다 큰 값의 위치를 반환
- 상한과 하한 값을 이용하여 중복 원소에 대한 길이를 알 수 있다.
중복 원소에 대한 길이 = 상한 - 하한
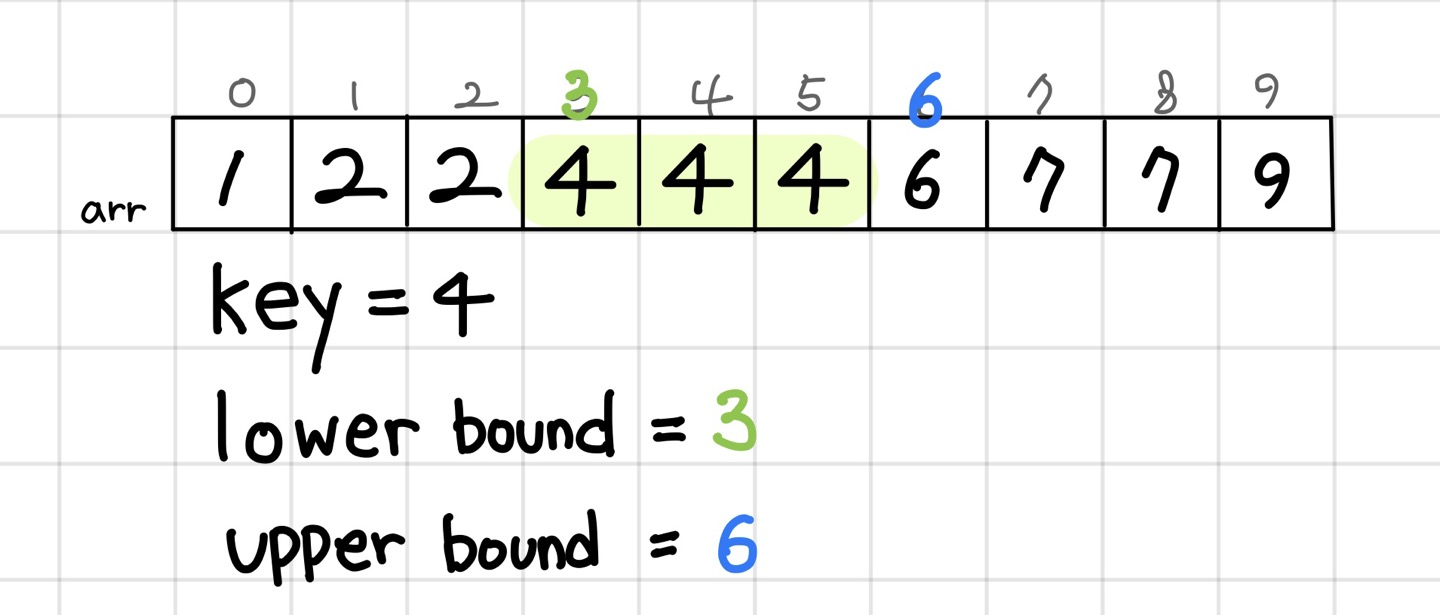
arr={1,2,2,4,4,4,6,7,7,9}; key=4 일 경우
lower bound = 3 (key 4 <= arr[3])
upper bound = 6 (key 4 < arr[6] )
static int lowerBound1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key <= arr[mid]) end = mid;
else start = mid + 1;
}
return start;
}
static int lowerBound2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key <= arr[mid]) end = mid - 1;
else start = mid + 1;
}
return start;
}
static int upperBound1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid;
else start = mid + 1;
}
return start;
}
static int upperBound2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else start = mid + 1;
}
return start;
}
정리하자면 아래와 같다.

public class LowerUpper정리 {
public static void main(String[] args) {
}
// 중복 고려
static int duplication(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start) / 2;
if(key <= arr[mid]) end = mid - 1; // 하한 (찾는 값 이상의 값의 위치)
if(key < arr[mid]) end = mid - 1; // 상한 (찾는 값 초과한 값의 위치)
else start = mid + 1;
}
return start;
// if(key < arr[mid]) 와 return end : 찾는 값 마지막 위치
}
// 중복 고려 X
static int notDuplicate(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start) / 2;
if(key < arr[mid]) end = mid - 1; // 상한 (찾는 값 초과한 값의 위치)
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return start; // key보다 크거나 같은 위치
// return end; // key보다 작거나 같은 위치
}
}
▼아래는 코드를 print로 테스트 해본 값들이다.
package BinarySearch;
import java.util.Arrays;
public class LowerUpper {
public static void main(String[] args) {
int [] arr = {1,2,2,4,4,4,6,7,7,9};
int [] arr2 = {1,2,2,4,4,4,4,4,7,9};
int [] arr3 = {1,3,5,7,9};
Arrays.sort(arr);
/* 중복 고려 */
// 있는 값
System.out.println(lowerBound1(arr,4)); //3 == 찾고자 하는 값 이상의 값이 처음으로 나타난 위치
System.out.println(lowerBound2(arr,4)); //3
System.out.println(upperBound1(arr,4)); //6 == 찾고자 하는 값을 초과한 값이 처음으로 나타난 위치
System.out.println(upperBound2(arr,4)); //6
System.out.println(upperBound3(arr,4)); //6
System.out.println(last1(arr,4)); //5
System.out.println(last1(arr2,4)); //7
System.out.println(last1(arr2,2)); //2
System.out.println(last1(arr,7)); //8
System.out.println(last2(arr,4)); //5 == 찾고자 하는 값이 마지막으로 나타난 위치
System.out.println(last2(arr2,4)); //7
// 없는 값
System.out.println(lowerBound1(arr,5)); //6
System.out.println(lowerBound2(arr,5)); //6
System.out.println(upperBound1(arr,5)); //6
System.out.println(upperBound2(arr,5)); //6
System.out.println(upperBound3(arr,5)); //6
System.out.println(last1(arr,5)); //5 == 찾고자 하는 값보다 작은 값 중 최대값의 마지막 위치
System.out.println(last2(arr,5)); //5
System.out.println(last2(arr,3)); //2
/* 중복 고려X */
System.out.println("---");
System.out.println(greaterThanOrEqualTo(arr3,5)); //2 == key 보다 크거나 같은 위치
System.out.println(greaterThanOrEqualTo(arr3,2)); //1
System.out.println(smallerThanOrEqualTo(arr3,5)); //2 = key 보다 작거나 같은 위치
System.out.println(smallerThanOrEqualTo(arr3,2)); //0
System.out.println(Arrays.binarySearch(arr,4)); //4 //있는 값
System.out.println(Arrays.binarySearch(arr2,4)); //4
System.out.println(Arrays.binarySearch(arr,3)); //-4 //없는 값
System.out.println(Arrays.binarySearch(arr,5)); //-7
//있는 값
System.out.println(binarySearch1(arr,4)); //5 == arr[mid]가 key랑 같을때 나타난 위치(별 의미 없음)
System.out.println(binarySearch2(arr,4)); //5
System.out.println(binarySearch1(arr2,4)); //5
System.out.println(binarySearch1(arr2,2)); //2
//없는 값
System.out.println(binarySearch1(arr,5)); // -1 == 없으면 -1 반환
System.out.println(binarySearch2(arr,5)); // -1
}
static int lowerBound1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key <= arr[mid]) end = mid;
else start = mid + 1;
}
return start;
}
static int lowerBound2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key <= arr[mid]) end = mid - 1;
else start = mid + 1;
}
return start;
}
static int upperBound1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid;
else start = mid + 1;
}
return start;
}
static int upperBound2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else start = mid + 1;
}
return start;
}
static int upperBound3(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid;
else start = mid + 1;
}
return end;
}
// 가장 뒤의 위치
static int last1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid;
else start = mid + 1;
}
return end-1;
}
static int last2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else start = mid + 1;
}
return end;
}
// 중복이 없을 경우 key 보다 크거나 같은 위치
static int greaterThanOrEqualTo(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return start;
}
// 중복이 없을 경우 key 보다 작거나 같은 위치
static int smallerThanOrEqualTo(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return end;
}
// 중복이 없거나 값의 유무를 고려해야할 경우의 이진 탐색
static int binarySearch1(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start < end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return -1;
}
static int binarySearch2(int [] arr, int key) {
int start = 0;
int end = arr.length;
while (start <= end) {
int mid = start + (end-start)/2;
if(key < arr[mid]) end = mid - 1;
else if(key == arr[mid]) return mid;
else start = mid + 1;
}
return -1;
}
}'공부 > 알고리즘' 카테고리의 다른 글
| [백준]11724_연결 요소의 개수_BFS Java 풀이(반례 포함) (0) | 2023.09.12 |
|---|---|
| [프로그래머스]12914_멀리 뛰기_DP Java 풀이 (0) | 2023.09.06 |
| [프로그래머스]42840_모의고사_완전탐색 Java 풀이 (0) | 2023.02.15 |
| [백준]20413_MVP 다이아몬드 (Easy)_그리디 Java 풀이 (0) | 2023.02.14 |
| [백준]1916_최소비용 구하기_다익스트라 인접행렬, 인접리스트 Java풀이 + 반례 (0) | 2023.02.08 |

댓글